how to make 3d printed dimension match drawing

When learning about existing mathematics, and especially when trying to produce new mathematics, we spend a lot of time thinking about examples. How do parts of the example interact with each other? What are the regularities and symmetries? Does it come in a family of examples, or does it alive on its own? In many cases, the first thing to do is to try and draw a picture. We are both geometric topologists, working mostly with two and 3-dimensional objects. As such, two-dimensional pictures are important currency in our field. These pictures are typically drawn on blackboards, on pieces of paper, and fifty-fifty on tablecloths and napkins, as famously depicted in Douglas Adams' word of Bistromathics.

A natural extension of drawing in ii dimensions is drawing in three dimensions. In this direction, we accept been using 3D printing as an aid to visualising mathematical objects. We design sculptures that help us and others to empathise the mathematics better. Also, these sculptures are beautiful in their own correct!

Here are a few favourite examples.

Half of a 120-cell

One-half of a 120-cell depicts a projection of the 120-prison cell, one of the four-dimensional regular polytopes (from the Greek — "poly" for many, "topos" for identify).

Effigy ane: One-half of a 120-cell, with views showing the ii-, 3- and 5-fold symmetries.

The familiar pentagon is a two-dimensional polytope having five facets, all of which are edges. The dodecahedron is a iii-dimensional polytope having 12 pentagonal facets. Finally the 120-cell is a four-dimensional polytope having 120 dodecahedral facets. In each example the facets are polytopes of one dimension lower.

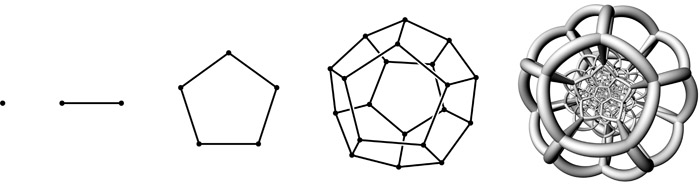
Figure ii: Polytopes of dimensions nothing through four: signal, interval, pentagon, dodecahedron, 120-prison cell.

To understand how to projection this four-dimensional object into three-dimensional infinite, we need to develop some intuition from lower dimensions.

In dimension two the corners of a foursquare sit on a circle which contains the whole shape. If we place a light at the center of the circle, the edges of the square cast shadows on the circle.

In dimension three, a cube sits inside a sphere. We arrange the cube and then that one of its square facets is horizontal, with the Due north pole directly in a higher place the facet'southward heart. Now we place a light at the centre of the sphere. The edges of the cube cast shadows onto the sphere, making a "beach ball cube". We delete the cube, and concentrate on the beach ball version. Move the light to the North pole. The edges of the embankment ball cube cast their shadows on the horizontal plane: the plane the sphere is sitting on. This last footstep is chosen stereographic projection, from the sphere to the plane. See figure 3 below for pictures of this procedure.

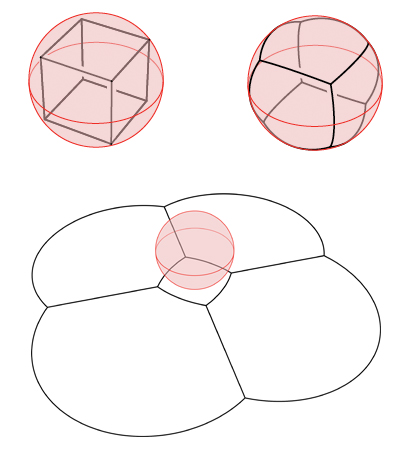
Effigy 3: Projecting a cube onto the aeroplane.

Finally, in dimension four, the 120-cell sits inside a three-sphere (the unit sphere in four-dimensional space). By casting shadows out from the center of the three-sphere nosotros make a "beach ball 120-jail cell". We use stereographic project to get the beach ball 120-cell into our ordinary iii-dimensional space. This gives the rightmost prototype in figure 2.

Note the massive complication near the center. This cannot exist printed using electric current technology — at least not inside our budget! We came up with the post-obit idea: we cut the projection of the 120-cell in half forth a sphere, and we threw away the outside. The outcome is shown in effigy one. Yous can find out more in this movie:

The internal structure is now visible. In improver, the ratio between the diameter and the smallest features is much more than reasonable, making the sculpture printable.

Quintessence

Afterwards playing with Half of a 120-cell for quite a while, we were inspired to design a family of interlocking puzzles which we call Quintessence; hither chains of dodecahedra living in the One-half of a 120-jail cell are combined to build diverse structures.

Effigy 4: Quintessence; copies of the six "rib" pieces shown in the pinnacle left can make all of these puzzles.

See how the puzzles work in this movie:

Figure 5: The reverse of a two pound coin.

Triple helix

Triple Helix (figure 6) is a machinery with iii helical gears, meshing in pairs, all at right angles to each other. There is an amusing mistake in graphic design, where three (or any odd number) of planar gears are bundled in a circumvolve. Perchance the best known example is the reverse of the two-pound coin (see figure v), designed past Bruce Rushin, which shows 19 gears that symbolise the Industrial Revolution. The mistake comes from the fact that neighbouring gears must rotate in opposite directions. Thus any circle with an odd number of planar gears is frozen! Triple helix is one solution to this paradox.

Figure 6: Triple helix.

Sentinel the triple helix motion:

Triple gear

Another, more complicated, solution titled Triple gear (effigy 7) involves using iii toothed-rings, all pairwise linked. Unlike our other work, these sculptures move. For much more on Triple gear and related mechanisms, check out our paper on the bailiwick, which appeared in the Proceedings of the 2013 Bridges conference on mathematics, music, art, architecture and culture.

Figure 7: Triple gear.

The triple gear in action:

Round Möbius strip

Round Möbius strip answers some other puzzle — it is a Möbius strip with a circular boundary! Famously, the Möbius strip can exist made by taking a long strip of paper, giving it a one-half-twist (twist by 180 degrees), and gluing the two curt edges together (run into this Plus commodity for more information). The resulting object has a single edge and one side. Different an ordinary piece of paper, you do not need to cross an border to go from one side to the other side. The purlieus of the paper Möbius strip describes a curve in space; this curve is non geometrically a circumvolve, but it tin be deformed into ane. This picture illustrates the thought:

Our sculpture shows what happens when you drag the surface of the Möbius strip along as yous "straighten out" the circle. Nosotros have also dragged 1 bespeak of the strip to infinity to bring out the symmetries of the Möbius strip, merely y'all can meet the round circle at the centre — this is the purlieus of the original Möbius strip.

Figure 8: The "round" Möbius strip.

3D printing

3D printing is a term that covers a number of closely related technologies, as well known as additive manufacturing. In all of these the idea is to build a physical object upwardly, layer by layer, starting from nothing. This contrasts with more traditional subtractive manufacturing, such as lathing or etching. Complicated internal structures are difficult to make in subtractive manufacturing, simply are easy in additive manufacturing. When subtracting, the object tin make it the mode of the carving tool. When adding, the impress caput always works from above, and at each moment the printed layers are below. Intricate details are now just a matter of persistence on the part of the designer; at the manufacturing stage it is equally easy to print a cake as it is to print a delicate filigree occupying the same volume.

The printing process is virtually entirely automated, which means that the printed object very closely approximates the calculator design. For u.s.a., this means that our prints are very close to the mathematical ideal. Many of our sculptures are entirely or almost entirely generated by (Python) lawmaking that direct expresses the desired geometry. Thus the mathematics described by our programs gets translated into concrete objects with very few choices or possibilities of error.

Withal, there are limits to what 3D printers can exercise. There is a basic tension between the minimum feature size and the overall size of a sculpture. As nosotros learned from the 120-cell, if some features are too small and then the sculpture volition accept parts that are fragile or peradventure just unprintable. The easiest solution to this trouble is to scale the design upward -- however if the resulting volume is too large the sculpture will be too expensive and maybe once again unprintable (if information technology does non fit inside the printer).

Getting into 3D printing is becoming easier and easier. These days many schools and universities, and even hobbyists accept 3D printers. There are also many 3D printing services that permit you upload a model, which they then 3D print and ship to you. In addition one of the states (Segerman) has given a workshop on 3D printing, using the programs Mathematica and Rhinoceros. The workshop materials are bachelor hither.

These include a preprint of the newspaper 3D printing for mathematical visualisation that appeared in the Mathematical Intelligencer.

Ideas for the hereafter

We are currently thinking most objects that move, or that can be taken apart and played with. Such sculptures play to the strengths of concrete objects equally opposed to pictures or even computer animations. As an instance of absurd stuff that wants to be 3D printed we mention planar linkages — a fascinating piece of engineering forth these lines is the Chaos machine of Robert MacKay. We are also thinking of sculptures based on hyperbolic rather than spherical geometry, and nearly the favourite knot of hyperbolic geometers, the figure-viii knot.

---

Almost the authors

Saul Schleimer is a geometric topologist, working at the University of Warwick. His other interests include combinatorial group theory and computation. He is especially interested in the interplay betwixt these fields and additionally in visualisation of ideas from these fields.

Henry Segerman is an banana professor in the Section of Mathematics at Oklahoma Country Academy. His mathematical enquiry is in iii-dimensional geometry and topology. He also makes mathematical artwork, often nigh geometry and topology, just likewise involving procedural generation, self-reference, ambigrams and puzzles.

kerbysupprionly1936.blogspot.com

Source: https://plus.maths.org/content/3d-printing

Share this post